초등학교 2학년에 들어서면 피타고라스의 정리를 이해하기위한 초석인
삼각형이 교과서에 등장하기 시작하여
초등학교 3학년에서 더 근접한 직각삼각형이 등장하며
중학교 3학년 과정에 가면 드디어 피타고라스의 정리가 본격적으로 소개되고
그 증명법과 다양한 활용을 공부하게 되는데 이 과정에 맞춰 무리수가 등장한다
무리수 역시 고교과정에 필수로 이어지고 수능 까지 연결되는 건 말할 필요도 없다.
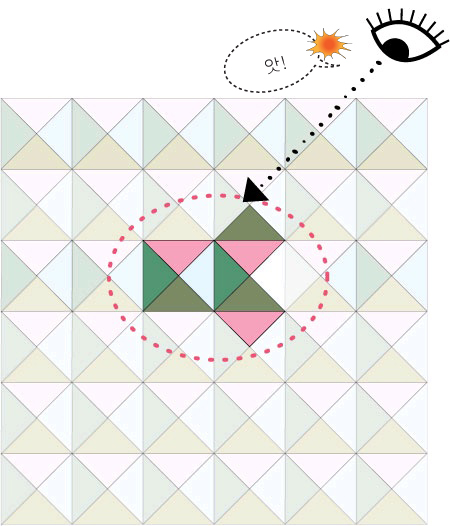
"콩콩 콩사마 수학스쿨"에 만화로 쉽게
여러 가지 방법으로 변화 되면서 반복 소개 되고 있는
피타고라스의 정리는 초등 학생도 충분히 이해할 수 있게 나와 있다
초등학생의 경우는 필히 "콩콩 콩사마 수학스쿨"에 나와 있는 피타고라스 정리를 충분히 읽은 후
아래에 나와 있는 정리 증명을 읽어 보기를 ......
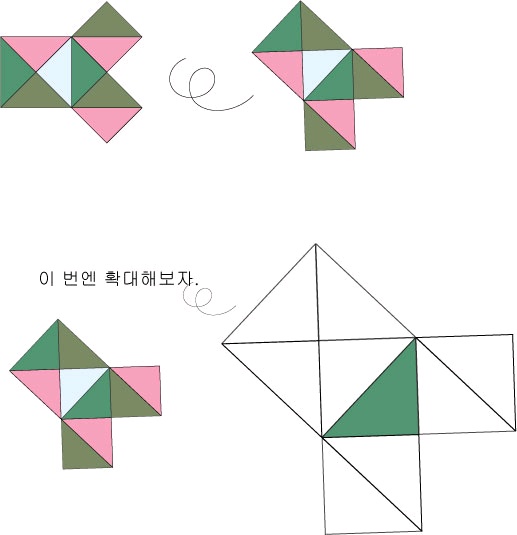
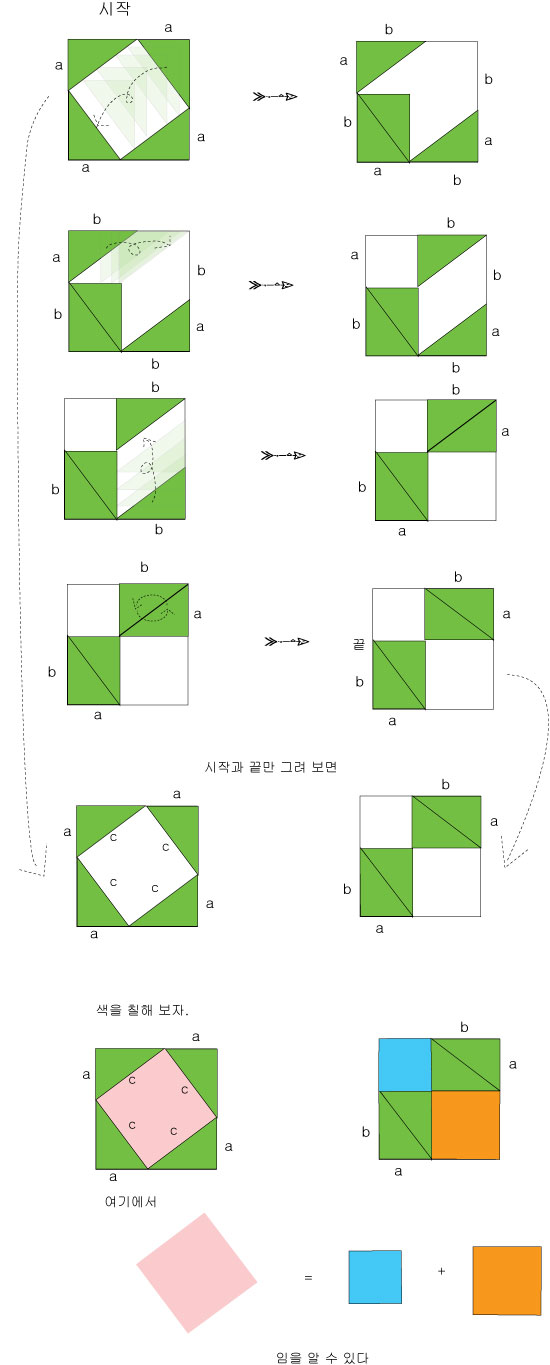
특히 아래의 피타고라스의 증명 1과 2는
거의 퍼
즐맞추기 식으로 증명하고 있기 때문에
초등학생의 경우에도 이해할 수 있다
피타고라스가 이집트로 유학을 갔을 때,
보게 된
|
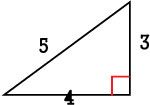
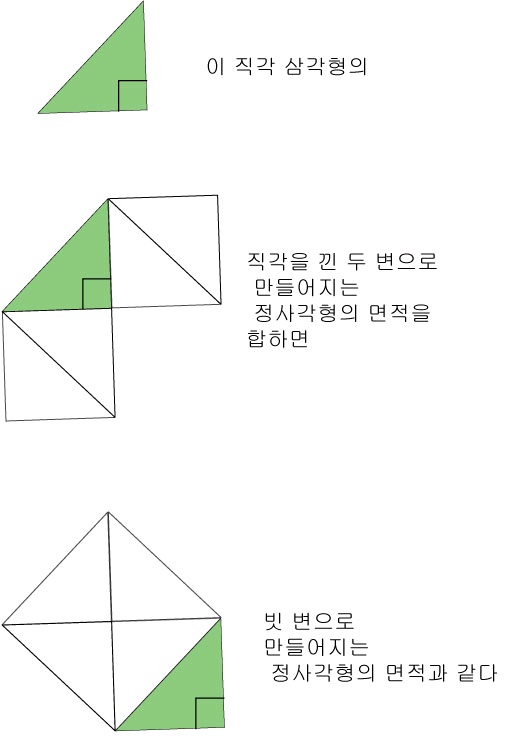
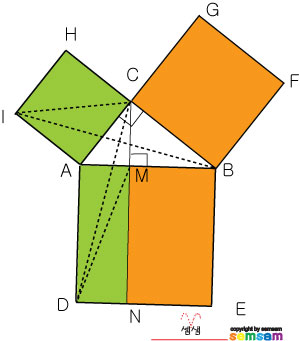
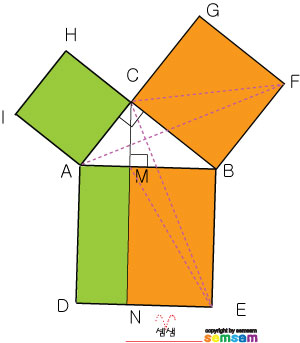
"직각삼각형의
빗변을 한 변으로 하는 정사각형의 넓이는
나머지 두 변을 각각 한 변으로 하는
두 정사각형의 넓이의 합과 같다"
|
|
조상 때부터 사용해 왔기 때문에 그냥 사용할 뿐이다
이집트 지식인의 말은 사실이었지만,
아래와 같은 이치를 터득하게 된다.
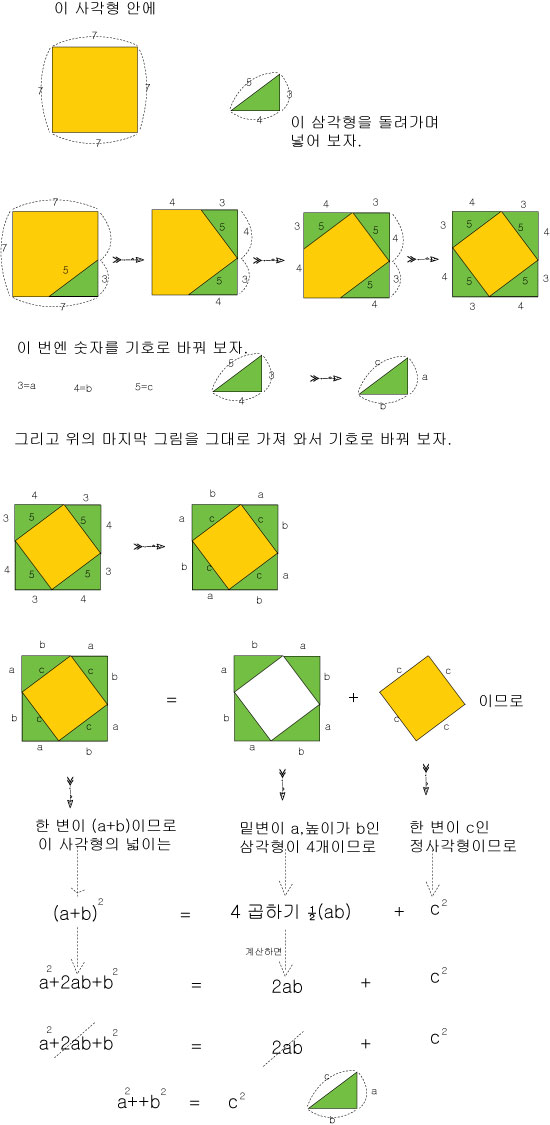
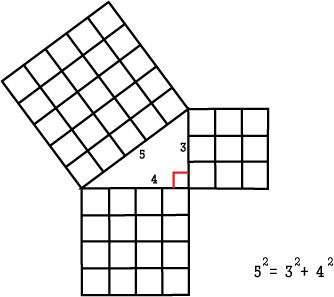 이번엔 다음 내용을 일반적인 식으로 써보자. 점점 어려워지는 것 같지만 중3 교과서에 나와 있는 내용이고,
그런 만큼 아직 중3이 아니더라도 한 번 쯤 봐 두는 건 필요하다.
그러다보면 기호로 된 식을 쉽게 이해하게 되는 데 도움이 된다
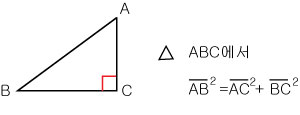 |
2500여년 전 에야 논리적 연구가 시작 되어왔던
증명방법이 수 천 가지라는데 20세기에 와서야
Elisha Scott Lomis 교수에 의해 정리 되었고,
피타고라스의 정리는 중국 수학책인 "주비산경” 에선 온 것으로
이는 피타고라스 보다 500년 앞선 기원 전 3000년이라 알려져있으며,
일반 건축물은 물론 이려니와